By: Keir Fogarty, Ph.D.
In the early 20th century, humankind’s understanding of the world of atoms and subatomic particles underwent a revolution; we went from understanding atoms as something like teeny billiard balls to the abstract concepts of quantum mechanics. In quantum mechanics, atoms and their constituent subatomic particles (electrons, protons, neutrons) have counterintuitive properties such as wave-particle duality, probabilistic behaviors, and other features that are difficult to imagine from our perspective in the macroscopic world. As the Nobel prize winning physicist Richard Feynman famously said, “I think I can safely say that nobody understands quantum mechanics.” Despite the abstractness of quantum mechanics, scientists use their understanding of quantum mechanical properties, most notably of electrons, to design better computers, lasers, and all manner of technology that benefit us in everyday life.
Richard Feynman was not only a Nobel prize winning physicist, he was also an avid bongo player.
At this point, you might be saying to yourself, “that opening paragraph was great and all, but I am no closer to understanding what the heck quantum mechanics is.” If that is what you’re saying, you are joining practically every introductory science student learning about the properties of electrons for the first time. What is quantum mechanics? Briefly; quantum mechanics is math. Quantum mechanics is a mathematical approximation of how always moving electrons, for example, “orbit” the nucleus of an atom. This mathematical approximation very accurately mirrors the experimental results of tens of thousands of experiments that we have performed in the real world.
So what does quantum mechanics tell us about the behavior of electrons? In the theoretical world of quantum mechanics, electrons are described by four-dimensional waves of particle probability. What?! Let’s compare this to waves in the ocean. Ocean waves are three dimensional waves of water, in that they have height, width, and breadth. Now visualize ocean waves that are coming into shore; most of the ocean water found near shore is found in the peaks of the waves. In the troughs of the waves, the water is shallow—there’s less of it—but in the peaks, the water is deeper. In the oceans, waves are three-dimensional shapes affecting the surface of the ocean, which is basically two-dimensional. Electrons are what largely give atoms their volume, and as we know, volumes are three-dimensional. Thus electrons, as described by quantum mechanics, look like waves in a three-dimensional surface (the fourth dimension is probability—in other words, the probability of finding an electron at a particular position at a particular time).
Enter CalcPlot3D! If we want to learn about the quantum mechanical behavior of electrons, it really, really helps to visualize what quantum mechanics predicts electrons “look like.” As every mathematician/math student knows, waves can be described by trigonometric functions like sine and cosine. CalcPlot3D absolutely excels at graphing functions in three-dimensions, and thus is perfectly suited to visualize three-dimensional electron waves, also known as orbitals. Pictured below are electron orbitals, as plotted in CalcPlot3D. Also pictured are 3D printed electron orbital models, which have been made by taking advantage of CalcPlot3D’s .stl file export option:
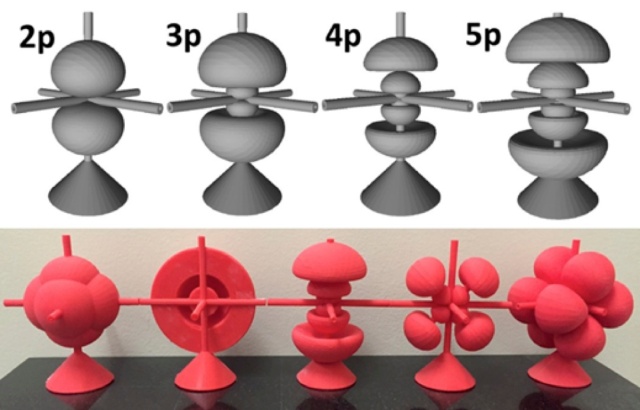
Top: orbitals created in CalcPlot3D, with their identification. The numbers refer to their energy level, and the “p” refers to their specific type.
Bottom: 3D-printed orbital models created through CalcPlot3D’s .stl file export tool. Several different types are pictured; s, p, d, & f
Pretty cool, right? Can you see how the electrons resemble three-dimensional waves? My chemistry students at High Point University made these awesome things, and you can too! If you want to learn how to, you can read the article we published in the journal of chemical education; Griffith, K. M.; de Cataldo, R.; Fogarty, K. H. “Do-It-Yourself: 3D Models of Hydrogenic Orbitals through 3D Printing.” Journal of Chemical Education 2016, 93 (9), 1586. Not only that, but if you access that article, it has all of the .stl files we generated using CalcPlot3D! You can 3D print almost 20 different models of electron-waves!
As I have said, that paper has a very detailed description of how we made the models, including step by step instructions in the supplemental portion of the article. However, it wouldn’t be fair if I didn’t talk a little about how these were made. These were made using two features in CalcPlot3D; the implicit surface tool, and the parametric surface tool. You might notice that, in addition to the “wavey” shapes of the electron orbitals, there are three cylinders, representing x, y, and z axes, as well as a cone, which serves as a base for the model. The axes cylinders and cones are created using the parametric surface tool in CalcPlot3D (actually, 4 separate parametric surface windows):
Once we have generated the axes cylinders and cone, we can generate the orbital using the implicit surface tool. Pictured below is a 2p orbital:
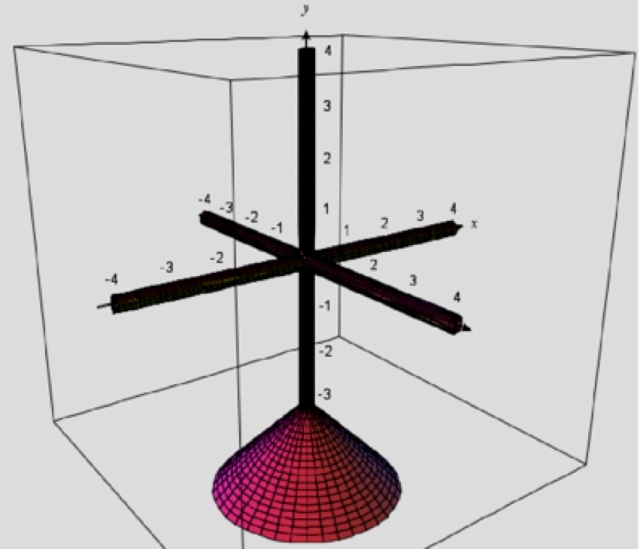
The axes cylinders and cone generated using the parametric surface tool
The 2p orbital pictured above was generated using the implicit surface tool in spherical coordinates, with adjustable parameters used to generate the shape in an appropriate scale:
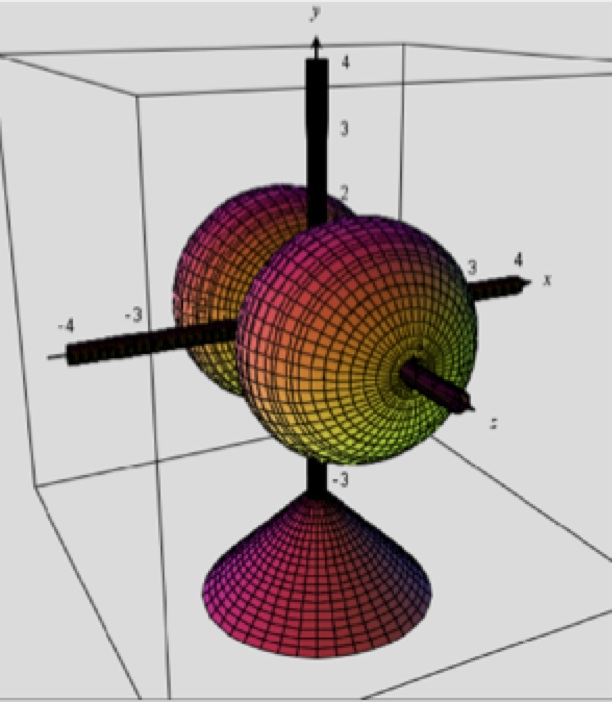
The 2p orbital generated using the implicit surface tool.
The awesome thing about CalcPlot3D is that it is so easy to generate visualization of complex mathematics in three-dimensions and then you can 3D print those awesome shapes. At High Point University, we use the CalcPlot3D models we create to help intro science students visualize the behavior of electrons in atoms.
This material is based upon work supported by the National Science Foundation under Grant No. 1524968, 1523786, and 1525216.
Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.
CalcPlot3D 